Physical Chemistry Laboratory [CHEM 335]
GAMMA - THE ADIABATIC EXPANSION METHOD
Jin Rei
ABSTRACT
The heat capacity ratios Cp/Cv of He and N2 have been determined by the adiabatic expansion method. The studies were performed using an 18.0 L carboy kept in a quasi-isothermal temperature modulated water bath at 298 K. Pressure measurements were made with a standard dibutyl phthalate manometer. The reliability of the results is quite good, with Cp/Cv values and the corresponding average 95% confidence limits for five measurements being 1.65 0.04 for He and 1.44 0.01 for N2. The Cp/Cv ratio for He agrees well with the theoretical value obtained from the classical equipartition theorem for a monatomic gas with three translational degrees of freedom. The experimental Cp/Cv ratio for N2 is closer to the theoretical value without vibrational contribution [7/5], than the corresponding value with vibrational contribution [9/7] due to the energy requirement of its vibrational mode, which according to our calculation, becomes fully active above 3395 K.
INTRODUCTION
For an ideal gas, Cp = Cv + R , where Cp and Cv are the molar heat capacities at constant pressure and volume, respectively. For an arbitrary real gas a slightly more complicated relationship between these heat capacities may be derived from the equation of state. The difference between heating a gas at constant volume and constant pressure is equal to the work of expansion. This ratio is denoted by the symbol gamma.
- Translational degrees of freedom: 3 independent coordinates specify the center of mass of the molecule.
- Rotational degrees of freedom: All molecules containing more than a single atom require specification of their orientation in space. Rotation of a diatomic molecule can be described by two rotational degrees of freedom since rotation about the internuclear axis leaves the molecule unchanged. Non-linear molecules require three rotational degrees of freedom.
- Vibrational degrees of freedom: The displacements of the atoms from their equilibrium positions can be described by 3N-5 DOF for linear molecules and 3N-6 for non-linear molecules. These values are determined by the fact that the total number of DOF must be 3N. For each vibrational DOF there is an associated normal mode of vibration of the molecule with characteristic symmetry properties and a characteristic harmonic frequency.
In classical statistical mechanics, the equipartition of energy theorem associates an energy of one half RT per mole with each quadratic term in the Hamiltonian or per degree of translational or rotational freedom [2]. Here, R is the Molar Gas Constant and T is the absolute thermodynamic temperature. A monotonic gas like He has no vibrational or rotational energy terms. As such, all energy must be contained in translational motion.
Where L is one of the dimensions of the container and n are principal quantum numbers. For a laboratory-sized container such as an 18.0 L carboy, the spacing between the energy levels is very small and the translational degrees of freedom can be treated classically. The electronic DOF associated with the possible configurations of electrons orbiting the atomic nuclei are frozen at room temperature. Similarly, nuclear degrees of freedom are frozen because they require activation energies far above what is available at room temperature. The only remaining DOF are rotational and vibrational. The rotational kinetic energy of a molecule is given by
Each vibrational mode behaves like an independent harmonic oscillator and contributes RT to the heat capacity of the gas. In general, a molecule containing N atoms has N -1 normal modes of vibration. For example, N2 has only one normal mode, corresponding to periodic stretching of the bond between the two nitrogen atoms. Thus, the classical contribution to the specific heat from vibrational degrees of freedom is
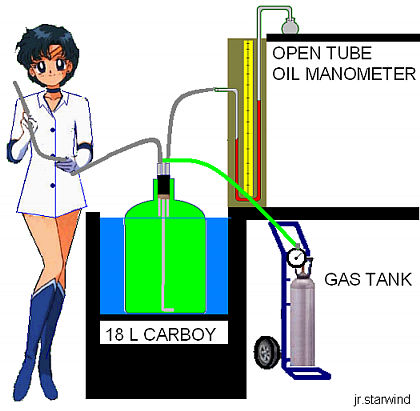
Figure 1. Setup for the Clement and Desormes method. The tube being held by the student is to be kept open to let the gas out of the container during the evacuation process and pressure adjustment prior to the first step of the experiment
A two step process can be used to experimentally determine γ [4]:
i. An adiabatic reversible expansion from the initial pressure P1, to the intermediate pressure, P2
EXPERIMENTAL SECTION
The adiabatic expansion experiments were carried out using the apparatus shown in Figure 1. The 18.0 L carboy was tied up (to avoid bouyancy) in a quasi-isothermal temperature modulated water bath at 298 K. The gas to be studied was swept through the carboy at a rate of 6 L/min for 10 min. The flow rate was measured by displacing 500 mL of water from an inverted Erlenmeyer flask held under water in the bath. In order to ensure complete evacuation of the air, the gas inlet was introduced down to the bottom part of the carboy during the process. Recall that He is lighter than air and leaving the gas inlet near the top of the carboy would create a body of helium floating in the air, affecting the evacuation process. The gas initially contained in the carboy was at a pressure P1 slightly higher than atmospheric pressure P2. The adiabatic reversible expansion was carried out by quickly removing and replacing the stopper in the carboy (step i). The gas remaining in the carboy was then allowed to return to its initial temperature T1 and final pressure P3 by heat transfer from the bath. The time allowed for this step was 15 min. The initial pressure P1, and the final pressure P3 were read using a standard dibutyl phthalate manometer. Pressure readings were converted to cm of Hg by multiplying the cm of dibutyl phthalate by the density ratio of dibutyl phthalate-to-mercury,
These were then added to atmospheric pressure to obtain the corrected P1, and P3. The thermodynamic expressions used to derive the heat capacity ratio apply only to the part of the gas that remains in the carboy after the stopper is replaced since molar volumes and molar heat capacities were used. Still, the reversibility of the expansion can be justified if one imagines an invisible surface separating the gas that remains within the carboy and the gas that escapes when the stopper is removed (Figure 2). The gas below this surface expands in an approximately reversible way against the surface. Work is done as the upper gas is pushed out. Where do we define the boundaries of the system? The Clement and Desormes method works reasonably well if the stopper in the carboy is replaced fast enough and the carboy throat diameter is between 2 and 3 cm. When these two conditions are met, a boundary can be clearly defined since the atmospheric pressure acts only outside the neck of the carboy.
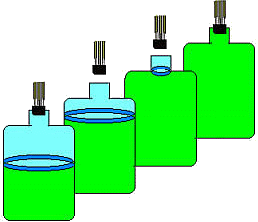
Figure 2. States of the expanding gas. The upper portion of the gas (the part that is let out) acts as a nearly massless piston. If the timing is just right, the process can be assumed to be adiabatic
RESULTS
To determine the [Cp / Cv] ratio, two different gasses were used: He and N2. The gases that were used had been swept through the carboy at a rate of 6 L/min for 10 min were protected against thermal flunctuations; which did not exceed 1.0 degrees when comparisons were made between T1 and T2. Since all pressures enter the calculations as ratios, the actual temperature is not as important as the difference between the initial and final state temperatures. Since this difference was rather small, all pressures were used without corrections for thermal flunctuations. A standard atmospheric pressure (7.60 cm of Hg) was added to the manometer readings after converting to cm Hg using Equation 19, for example:
cm Hg = 27.5 cm of db phthalate X {[1.046 g/cm3] / [13.5 g/cm3]} = 2.13 cm of Hg
Corr Pressure = 2.13 cm of Hg + 7.60 cm of Hg = 9.73 cm Hg
[Cp / Cv] ratios were computed using Equation 18 and setting P2 equal to 7.60 cm Hg. For P1 equal to 9.73 cm of Hg and P3 equal to 8.38 cm of Hg we get:
γ = ln [9.73 cm of Hg /7.60 cm] / ln [9.73 cm of Hg /8.38 cm of Hg]
γ = 1.65
The [Cp / Cv] ratio was determined five times for each gas, the values reported in Table 1 are the average values of each data set:
Av. [Cp / Cv] for He = [1/5] X [1.59 + 1.65 + 1.66 + 1.69 + 1.65] = 1.65
The corresponding 95% confidence limits were obtained using t = 2.13 for four independent measurements.
S2 for He = [1/4] X [(1.59-1.65)2 + (1.65-1.65)2 + (1.66-1.65)2 + (1.69-1.65)2 + (1.65-1.65)2]
S2 for He = [1/4] X [(-0.06)2 + (0.00)2 + (+0.01)2 + (+0.04)2 + (0.00)2]
S for He = 0.0364
[λ95] for He = [0.0364 X 2.13] / √5 ≈ +/- 0.04
Since for an ideal gas, Cp = Cv + R , and from Equation 1, Cp/Cv = γ. The experimental heat capacities (EXP Cp and Cv in Table 1) were obtained from the average values of γ.
Cv for He = R / [γ-1] = [8.31 J/mol*K] / [1.65 -1] = 12.78 J/mol*K
Cp for He = Cv + R = [12.78 J/mol*K] + [8.31 J/mol*K] = 21.09 J/mol*K
Our experiments indicate that the heat capacity can be predicted reasonable well for ideal gasses. As shown in Table 1, the He data set fits all the thermodynamic parameters when rounded off to the first decimal place, which is within the limit of the equipments capabilities. Although the thermodynamic parameters for N2 seem a little off, the value for γ is very close to the prediction of the equipartition of energy theorem if the N2 vibrational modes are assumed to be frozen out.
| GAS | PRED γ | ΩLIT Cv (J/mol*K) | ΩLIT Cp (J/mol*K) | EXP γ | EXP Cv (J/mol*K) | EXP Cp (J/mol*K) |
| He | 5/3 | 12.81 | 20.79 | 1.65 0.04 | 12.78 | 21.09 |
| N2 | 9/7; Ψ7/5 | 20.82 | 29.13 | 1.44 0.01 | 18.89 | 27.20 |
ΩFrom P. Atkins, "Physical Chemistry", 5th ed., W. H. Freeman, New York (1994).
ΨWithout vibrational contribution.
DISCUSSION
In the present study the Clement and Desormes method was employed to determine the [Cp/Cv] ratio for gasses. In an effort to highlight the differences between an ideal gas with three degrees of translational freedom and a nonideal gas possessing vibrational in addition to translational degrees of freedom, two different gasses (He and N2) were used. The heat capacities were predicted with different degrees of error, which reflect the differing ideality (or nonideality) these two gasses. Nevertheless, the [Cp/Cv] ratios agreed considerably well with those obtained using the equipartition of energy theorem. The differences can presumably be attributed to the differing sensitivities of the Clement and Desormes method and the degree to which the process was kept adiabatic. For example, differences in carboys neck diameter will allow different amount of heat exchange between the air in the room and the gas in the carboy. The time during which the carboy is kept open to the atmosphere will also affect the results: if the time is too short, the gas will not drop to atmospheric pressure and value of γ will be high; if the time is too long, the gas will exchange thermal energy with the air in the room and value of γ will be low.
In addition to the possible experimental errors, the extent to which the vibrational degrees of freedom contribute to the results cannot be ignored. From Equation 8, the classical contribution to the specific heat from vibrational degrees of freedom [N - 1]RT, where N is the number of atoms in the molecule. Thus N2 is predicted to have an RT J/mol*K contribution from its single vibrational mode. However, our results indicate that this vibrational mode is not fully active. At what temperature Θvib will the vibrational contribution attain its classical equipartition value? To answer this question, the vibrational contribution Cvib was rewritten in the form [3]
Where Θvib is the critical high temperature limit and can be obtained from
Where h is Planks constant, c is the speed of light, υ is the energy required to activate the vibrational mode of N2, and k is the Boltzmann constant. Using υ = 2358 cm-1 [5] we get:
Θvib = [6.626 X 10-34 J/s] X [3.00 X 1010 cm/s] X [2358 cm-1] / 1.380 X 10-23 J/K
Θvib = 3395 K
The Cvib contribution to the heat capacity at 278 K was then predicted from Equation 20.
Cvib = R {[(3395 K / 298 K) e-(3395 K / 596 K)] / [1 - e-(3395 K / 298 K)]}
Cvib = R {3.825 X 10-2} = 0.3178 J/mol*K
It can be seen from Table 1 that these are pretty accurate predictions for N2. The freezing out of vibrational degrees of freedom becomes gradually less effective as molecules become heavier and more complex. This effect can be accomplished by either weakening of the chemical bond (decreasing the force constant) or increasing the molar mass (increasing the effective mass).This accounts for the non-classical heat capacity of N2. Here, the vibrational mode contributes to the heat capacity by a value less than R because the temperature is not high enough.
BIBLIOGRAPHY
[1] D. Shoemaker, C. Garland, and J. Nibler, Experiments in Physical Chemistry", McGraw-Hill, New York, (1995)
[2] H.C. Corben and P. Stehle, Classical Mechanics, 2nd ed., Dover Publications, New York (1960)
[3] P. Atkins, "Physical Chemistry", 5th ed., W. H. Freeman, New York (1994)
[4] M. France, "Lab Manual for Physical Chemistry" , D. Van Nostrand Company, New York (1928)
[5] D.A. McQuarrie and J.C. Simon, Physical Chemistry A Molecular Approach, University Science Books, Sausalito, CA (1997)
APPENDIX A: RAW DATA FOR N2

APPENDIX A: RAW DATA FOR He



