THERMOCHEMISTRY

Energy is often defined as the ability to do work, and can be classified as either energy of motion (Kinetic), or energy of position (Potential). The SI unit of energy is the Joule (J). This is a derived physical quantity having dimensions of mass X length2 X time-2.

The internal energy change of a system of particles can be measured in terms of the work done on/by the system and the heat transfered in/out of the system,

dU = dq + dwexp + dwother

This equation is often applied to the first law of thermodynamics. This law states that the energy of the universe remains constant, or energy can be neither created nor destroyed, only changed from one form of energy to another. The sign of dq, and dw, indicates the direction of the flow of energy (+ means in, - means out). The thermodynamic variable we have referred to as internal energy is a state function, which means that the outcome will result independent of the path taken from the initial to final state.
We define dwexp as the work done by a system expanding against an external pressure,
dwexp = -pextdV = -p dV

and dwother is non expansion work (such as electrical work). Thus the change in internal energy of a system is equal to the amount of heat supplied if the system does not do any type of non-expansion work and its volume does not change,
dU = dq if dwexp = 0, and dwother = 0

And for measurable changes ΔU = qv, where qv is the constant-volume heat capacity. That type of measurements are done with a bomb calorimeter. But in the general chemistry laboratory, all work will take place under the influence of a constant atmospheric pressure. Now the internal energy of the system is not equal to the amount of heat supplied because the system is free to change its volume. This quantity is equal to the change in the enthalpy of the system. We will be concerned with situations where the only allowed type of work is expansion work, thus the change in enthalpy is equal to the thermal energy input/output. We can obtain the internal energy change from the enthalpy,
ΔH = ΔU + pΔV

So if we know the enthalpy change, the volume change, and the external pressure of the system, we can compute the internal energy change. From the ideal gas law we obtain pV = nRT or pΔV = ΔngasRT, and the enthalpy equation becomes:
ΔH = ΔU + ΔngasRT

The pΔV contribution for condensed phases (liquid, solid) is very small and can be ignored. This is not so for reactions that consume or produce gasses.
ΔH can be measured using an isobaric calorimeter.

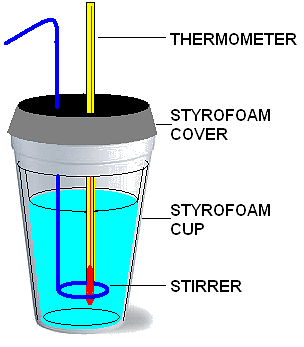
A low-tech isobaric calorimeter

ΔH Enthalpy is also defined as heat flow, and heat is a type of energy known as thermal energy. This type of energy is related to temperature but is not the same as temperature, since thermal energy may be used for something other than increasing temperature. For example, phase changes absorb/release thermal energy but the process does not envolve a temperature change.

Depending on the type of material, different amounts of thermal energy are required to induce a particular temperature change. We define the thermal energy required to increase the temperature of 1 gram of substance by 1 0C as its specific heat. Thus the thermal energy Q required for a temperature change ΔT can be obtained from

Q = m Csp ΔT

where m is the mass in grams and ΔT = [T2-T1]. Similarly, the thermal energy Qmolar required to increase the temperature of 1 mol of substance by 1 0C is defined as its molar heat capacity Cmolar and can be calculated from
Qmolar = n Cmolar ΔT

where n is the number of moles.

For chemical reactions that involve a change in enthalpy ΔHrxn is the energy per mole of reaction Qmolar. Exothermic reactions release energy into the surrounding and are designated by a negative sign on the ΔHrxn. Endothermic reactions take energy from the surroundings and are designated by a positive value of ΔHrxn. The sign of Q is the opposite to that of ΔHrxn because it refers to the change in state of the system where the reaction takes place.

Calorimetry is an experiment to measure Q by measuring temperature change. The heat capacity of the calorimeter is used to convert temperature change to thermal energy. The reaction has to occur in a calorimeter and energy will be transfered to it. Since the system is then comprised of the calorimeter and its contents, the specific heat of the entire system must be known from a calibration step.

CALIBRATING AN ISOBARIC CALORIMETER
We start by defining the heat capacity of the system,

Csys = Csol + Ccal

where Csol is the heat capacity of the solution and Ccal is the heat capacity of the empty calorimeter. Csys can then be obtained from,
Qknown / ΔT = Csol + Ccal

where Qknown is a known amount of thermal energy generated or consumed by a standard.

Example for the heat capacity of an isobaric calorimeter

The acid base neutralization:

NaOH(aq) + HCl(aq) --> NaCl(aq) + H2O ΔHrxn = -56.2 X 103 J

was employed in the standardization of an isobaric calorimeter. The amounts of each reactant added to the reaction vessel were 100 X 10-3 L of 0.5 M HCl and 200 X 10-3 L of 0.5 M NaOH. The initial temperature of both solutions was 21.5 0C initially. The final temperature of the solution mixture was 23.1 0C. Determine the heat capacity of the empty calorimeter. 

mol of NaOH = 200 X 10-3 L X 0.500 mol/L = 100 X 10-3 mol

mol of HCl = 100 X 10-3 L X 0.500 mol/L = 50.0 X 10-3 mol

From the reaction stoichiometry, each mol of HCl reacts with one mol of NaOH. Since the amount of HCl is smaller, HCl is limiting.

Since the energy is being released by the reaction ΔHrxn is negative. This energy is being transfered into the system so Qknown has a positive sign.

ΔHrxn = -Qknown

ΔHrxn refers to the amount of thermal energy released by the neutralization of 1 mol of NaOH by 1 mol of HCl, but the actual amount of neutralized material is 50.0 X 10-3 mol. So the actual Q value is 

Q = Qknown X n

Q = 56.2 X 103 J/mol  X 50.0 X 10-3 mol = 2.81 X 103 J

The heat capacity of the system is, 

Csys = 2.81 X 103 J / [23.1 - 21.50] 0C = 1.76 X 103 J/0C
Assuming the solution has the same specific heat as pure water,
Csys = [CspH2O X m H2O] + Ccal

Assuming the solution has the same density as pure water (true for very dilute solutions),
m H2O = [200 X 10-3 L + 100 X 10-3 L] 1000 g/L = 300 grams
And the heat capacity of the solution mixture is, 
CspH2O = [4.184 J/0C X g] X 300 grams = 1.26 X 103 J/0C = Csol
Thus the heat capacity of the empty calorimeter is, 
Ccal = Csys - Csol

Ccal = 1.76 X 103 J/0C - 1.26 X 103 J/0C = 0.500 X 103 J/0C


EXPERIMENTAL PROCEDURE
I. CALIBRATION

Put together your isobaric calorimeter. If you have two thermometers, one should be used for each solution prior to mixing, if you have only one thermometer, rinse the probe with DI water and dry it with a paper towel between readings. Record the temperature of the NaOH solution at time = 0 min, record the temperature of the HCl solution at time = 1 min. Repeat the process up to time = 5 min, then pour the NaOH solution (beaker) into the HCL solution (styrofoam cup). Keep recording the temperature up to time = 20 min. The calibration of your isobaric calorimeter will require the following reagents:

Container Solution Molarity [mol/L] Volume [L]
beaker NaOH 2.0 50.0 X 10-3
styrofoam cup HCl 2.0 50.0 X 10-3
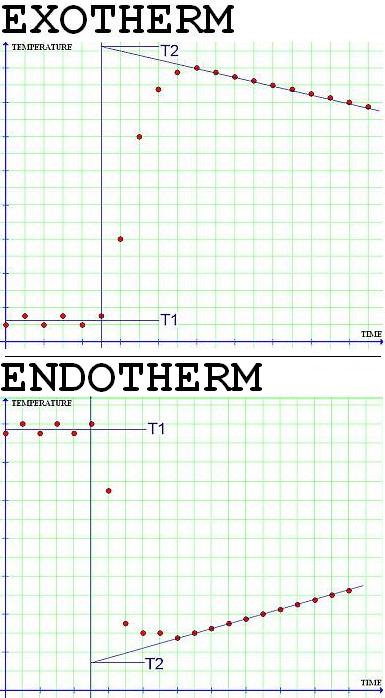
Plot the temperature readings in the ordinate and time in the abscissa,

The graph should resemble the [exotherm] in the above figure because ΔHrxn is negative for this specific neutralization reaction. Since the time of mixing was t = 5 min, the value of ΔT should be read at that point in time. To do that,

  • Draw a line perpendicular to the fifth minute point. Now the datapoints are divided into pre- and post-reaction readings.
  • Draw a line through the six datapoints prior to the time of mixing, this line will intercept the line perpendicular the the fifth minute point at T1.
    -Draw a line through the last set of datapoints (after the temperature inflection point), this line will intercept the line perpendicular the the fifth minute point at T2.
    Then ΔT is obtained from,
    ΔT = [T2 - T1]

    II. MOLARITY OF UNKNOWN NaOH

    The experimental procedure is basically the same as the calibration step. Now we will use our calorimeter and the known ΔHrxn to determine the molarity of a NaOH solution.

    NaOH(aq) + HCl(aq) --> NaCl(aq) + H2O ΔHrxn = -56.2 X 103 J J

    For this we will need the following reagents:

    Container Solution Molarity [mol/L] Volume [L X 10-3]
    beaker NaOH ? 40.0
    styrofoam cup HCl 2.0 40.0

    You saw in the calibration example that the number of moles of the limiting reagent determine the energy output of the reaction. For the HCl neutralization by NaOH,

    -56.2 X 103 J = ΔHrxn = ? -Qknown

    Where -Qknown is is the energy output for one mole of product. The actual output is the output per mol times the number of mol,
    -Q = -Qknown X n

    Thus we can compute the number of mol of product which is also the number of mol of the limiting reactant, which in this case will be NaOH,
    -Q / -Qknown = n

    The molarity of NaOH is given by, 
                number of mol of NaOH 
m(NaOH)  = -----------------------
             v(NaOH) in Liters

    II. ENTHALPY OF FORMATION OF MgO

    Some enthalpies of reactions are very difficult to measure experimentally or their setup is physically impossible. These enthalpies can be determined using Hess's law: if a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps. Thus the reaction,

    Mg(s) + 1/2 O2 (aq) --> MgO(s)

    Can be expressed as the algebraic sum of three reactions, 
    ΔH1   =    ?    Mg(s) + 2H+           -->  Mg2+(aq) + H2(g)
ΔH2   =    ?        Mg2+(aq) + H2O(l) -->  MgO(s) + 2H+(aq)
ΔH3   = -285.85 kJ/mol    1/2 O2(g) + H2(g)     -->  H2O(l)

    Hess’s law works because enthalpy is a state function; it depends only upon the initial and final state of the reactants/products and not on the specific pathway taken.

    To determine ΔH1we will need the following reagents:

    styrofoam cup 60.0 mL of 2.0 M HCl
    weighting boat ~0.18 Granulated Magnesium

    The pre-reaction data points will be provided by the temperature of the HCl solution taken for t = 0 to t = 5 min. On the fifth minute add the Magnesium into the calorimeter and put the lid on. Stir the mixture and continue to take the temperature at 1 min intervals until all the spaces on your data sheet are used up. Display your data graphically and determine the thermal energy input/output using,

    Q = m Csp ΔT

    And ΔHrxn is given by,
    ΔHrxn = -Q/n

    Notice that the sign of Q is reversed because ΔHrxn refers to the reaction and Q refers to the system. The number of mol of Magnesium is obtained using its molar mass and the number of grams of granulated Magnesium.

    To determine ΔH1we will need the following reagents:

    styrofoam cup 60.0 mL of 2.0 M HCl
    weighting boat ~1.00 grams of Magnesium Oxide

    The procedure is the same as for ΔH1 but notice that the sign is reversed for this enthalpy value. The required reaction for the Hess’s law calculation is, 

    ΔH2 = ?  Mg2+(aq) + H2O(l) -->  MgO(s) + 2H+(aq)
    Whereas the reaction we are carrying out is, 
    -ΔH2 = ?  MgO(s) + 2H+(aq) --> Mg2+(aq) + H2O(l)