When a new compound is discovered, us chemists would like to have its formula determined. The word formula on its own has various meanings; here we are refering to the relative amount of each element for a given amount of compound. There are various ways of representing the relative amount of each element for a given amount of compound, these lead to MOLECULAR formulas and EMPIRICAL formulas. There are some concepts we should be familiar with before the experiment is carried out...
MASS PERCENTAGE
[mass of γ in the whole]
The percentage of γ = -------------------------- X 100
[mass of the whole]
Example using mass percent
NH4NO3 = [14 X 2] + [1 X 4] + [16 X 3] = 80.0 g/mol
Compute the mass percentage of the elements in ammonium nitrate, NH4NO3
% N = [(14 X 2) / 80.0] X 100 = 35.0%
% H = [(1 X 4) / 80.0] = 5.00%
% O = [(16 X 3) / 80.0] = 60.0%
EMPIRICAL FORMULAS
The mass percentage was just obtained from an EMPIRICAL FORMULA, so the inverse process would yield an empirical formula from mass percentage. An empirical formula is the formula of a compound written with the smallest whole number subscripts.
Example obtaining empirical formula
A compound contains the following mass percentages: 69.6% O, and 30.4% N. What is the empirical formula?
The ratio N:O is 1:2, so the empirical formula is NO2
mol of O = [69.6 / 16] = 4.35
mol of N = [30.4 / 14] = 2.17
O 4.35 --> 4.35 / 2.17 = 2.00
N 2.17 --> 2.17 / 2.17 = 1.00
MOLECULAR FORMULAS
The empirical formula is sometimes the molecular formula of the compound, as is the case in the above example. However, the molecular formula is unique for a particular compound, while many compounds might have the same empirical formula.
Example obtaining empirical and molecular formula
Certain compound is 39.9% C, 6.7% H, and 53.5% O. Determine the empirical formula. The molar mass of this compound is 180.0 g/mol. What is its molecular formula?
The ratio C:H:O is 1:2:1, so the empirical formula is CH2O
mol of C = [39.9 / 12.0] = 3.3
mol of H = [6.7 / 1.00] = 6.7
mol of O = [53.5 / 16.0] = 3.3
C 3.3 --> 3.3 / 3.3 = 1.0
H 6.7 --> 6.7 / 3.3 = 2.0
O 3.3 --> 3.3 / 3.3 = 1.0
Then we use:
Molar Mass = Number of Moles X Empirical Formula Mass
where the Number of Moles is the number of empirical units that fit into the molar mass of the compound, and the empirical formula mass is the sum of molar masses of the component elements in one empirical unit:
C + [2 X H] + O = 12.0 + [2 X 1.00] + 16.0 = 30.0 g/mol
And the molecular formula can then be obtained. First we obtain the number of empirical units that fit into the molar mass of the compound:
n = MM / EFM = 180.0 / 30.0 = 6.00
So the empirical unit fits six times in the molar mass of the compound.
CH2O X 6.00 = C6H12O6
STOICHIOMETRY
This is a fundamental part of quantitative work in chemistry and is based on the notion that an equal quantity of matter exists both before and after a reaction. To understand the concept, let's consider the reaction:
Until more advanced concepts are covered, the physical state of the compounds (solid, liquid, gas, plasma) are not to be considered important. Just notice that the equation is balanced:
For the reactants,
There is a number 1 on front of WO <-- no number means 1
There is a number 3 on front of H2
For the products,
There is a number 1 on front of W
There is a number 3 on front of H2O
The chemical equation can be translated into other formats:
231.84 g of WO3(s) + 6.00 g of H2(g) --> 183.84 g of W(s) + 54.00 g of H2O(g)
The equation is balanced, that is how we know that the given amounts will produce 1 mol of W(s). If the amount of WO3(s) were increased to 4 mol while keeping the amount of H2(g) constant we would still get 1 mol of W(s) because H2(g) is LIMITING. In order to use up the 4 mol of WO3(s) we would need 12 mol of H2(g) so that none of the reagents is limiting.
The predictive power of stoichiometry is derived from its ability to connect the submicroscopic and the macroscopic world. Note that 3 mol of H2O weights 54.00 grams, each mol amounts to 6.022 X 1023 molecules of H2O. There is nothing special about this number, the concept was conceived before the actual value was determined. The following two statements are equivalent and will better illustrate the concept:
THERE ARE 6 BEERS IN ONE SIX-PACK OF BEERS.
THERE ARE 6.022 X 1023 ATOMS IN ONE MOLE OF ATOMS.
None of these statements provides information about the mass of the six-pack of beers or the mole of atoms. For example, if you go to the store and buy a six-pack of 11-ounce beers, then the six-pack would weight 66 ounces. If you decide to get the 20-ounce beers six-pack, then the six-pack would weight 120 ounces. And it is still a six-pack.
The same can be said about the mole of atoms: one mole of Neon atoms weights ~20 grams, one mole of Calcium atoms weights ~40 grams. And it is still one mole.
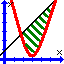
For this experiment, consider a cation Φn+ whose oxidation state and molar mass are unknown. Such a cation will form an insoluble compound with certain ligand. Here we will use oxalic acid as the source of the oxalate ligand:
Only the oxalate anion is of interest here, as discussed in class, the oxalate anion has two negatively charged ends...

and will combine with the cation in a way as to neutralize the charges...
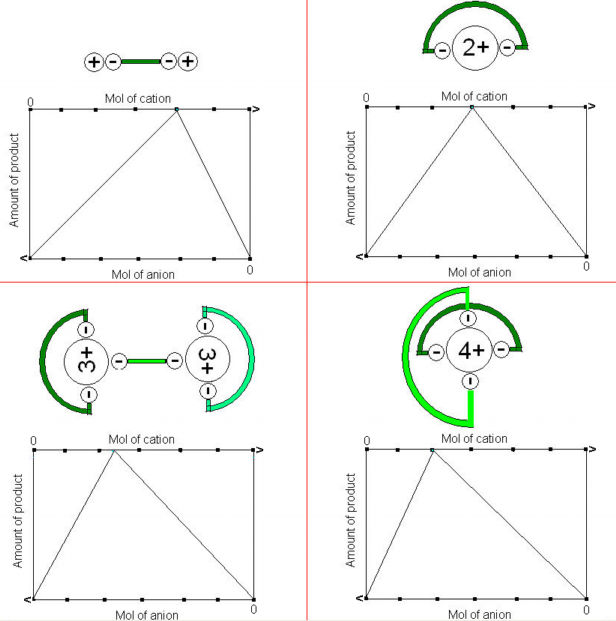
Then it is clear that if you combine different amounts of Φn+ and C2O42- they will combine and form an amount of product proportional to the amount of limiting reagent. There will be one combination of Φn+ and C2O42- that will allow all of the reagents to be used up and form the maximun amount of product. That combination is predicted by the apex point of the plot of grams of product as a function of Φn+:C2O42- ratio.
In this experiment, different amounts of 0.100 M solutions of Φn+ and C2O42- will be combined. The number of moles of reagent can be obtained by,
where the units of volume are Liters.
EXPERIMENTAL PROCEDURE
Each group will obtain
Rinse buret labeled "Unknown" with DI water, then with a small amount of 0.100 M Φn+ solution, you have been given enough solution so that there is a few mL extra. Do the same with the buret labeled "Acid" using the C2O42- solution.
Dispense the Φn+ and the C2O42- solution into each of the 50.0 mL beakers. The recommended amounts are:
| Beaker # | I | II | III | IV | V | VI |
| mL of 0.100 M Φn+ | 4.00 | 6.00 | 8.00 | 16.00 | 18.00 | 20.00 |
| mL of 0.100 M C2O42- | 20.00 | 18.00 | 16.00 | 8.00 | 6.00 | 4.00 |
Note that the total volume of each solution is 24.00 mL. The burets have a readability limit of one hundreth of a mL (+/-0.01 mL) so you are expected to do measurements with such precision. The burets are labeled 0.00 at the top and 50.00 at the bottom...
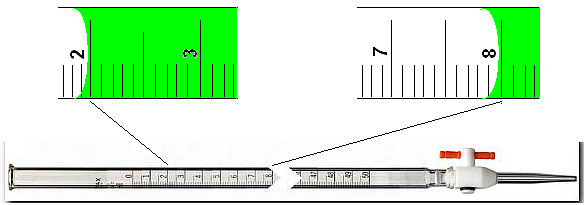
Reading 1: 2.00, Reading 2: 8.00
Volume delivered 6.00 mL
For a 6.00 mL sample of solution whose concentration is 0.100 M, the number of mol is
For a 22.00 mL sample of solution whose concentration is 0.100 M, the number of mol is
Then the number of mol being combined in each trial are
| Beaker # | I | II | III | IV | V | VI |
| Mol Φn+ X 10-4 | 4.00 | 6.00 | 8.00 | 16.00 | 18.00 | 20.00 |
| Mol of C2O42- X 10-4 | 20.00 | 18.00 | 16.00 | 8.00 | 6.00 | 4.00 |
Heat the solutions for ~ 5 min, remove from heat and allow them to cool to room temperature. The product is an insoluble salt. Suction filtration will be employed to separate the solid phase that precipitates from the solution.

The vacuum filtration assembly.
The laboratory is equipped with aspirators that permits access to a vacuum while water is flowing through. This is a practical application of Bernoulli’s Principle; which describes the reduced pressure caused by a flowing fluid when it passes through a constriction. You will be required to determine the mass of the precipitate. To do that determine the mass of each [filter paper + weighting boat]. This mass must be substracted from the total mass once the solid is recovered,
m(solid) = m[filter paper + weighting boat + solid] – m[filter paper + weighting boat]
Rinse the filter flask and the Buchner funnel. Make sure the filter is clean before each separation. Set up a ring stand with a clamp and secure the flask at its neck. The flask should rest on the base of the ring stand. Connect the side arm of the filter flask to the side arm of the aspirator using heavy-walled rubber tubing. Place the rubber stopper which holds the bottom part of the Buchner funnel in the top of the suction flask.Place a piece of filter paper, centered and completely flat, against the perforated surface of the funnel. At this point it is assumed that you have the mass of the dry filter paper written somewhere. Pour the liquid from the beaker containing the desired precipitate. It should be poured slowly and directing the solution and precipitate to the center of the filter paper. Wash the remaining solid in the beaker using a small amount of water from a wash bottle. Do not use more water than is absolutely necessary or you may begin to dissolve some of the precipitate that you have already accumulated. Keep the aspirator running for a while after the last amount of liquid has been transferred to the funnel. Add a few drops of acetone; this helps to dry it faster. Use a spatula to separate the filter paper from the funnel. Scrape any solid that remains in the funnel, the solid might fall onto the weighting boat (not on the filter) but this does not affect the results.
Following its recovery, the solid must be air dried. Weight the product for each combination of Φn+ and C2O42- solutions once the precipitate is as dry as desired. For the cation and reagent amounts used here, the product should be no heavier than ~0.18 g and no lighter than ~0.03 g. Excessively high apparent yields can result if the product is inadequately dried, while low yields are typically caused by using too large a volume of water during the filtering step.
DATA PROCESSING
# grams of product
molar mass of product = --------------------
# of moles of product
molar mass of Φn+ X N] = molar mass of product
- [molar mass of C2O42- X M]
[molar mass of Φn+ X N]
molar mass of Φn+ = --------------------------
N