UV-VIS SPECTROMETRY
Spectrometry is the use of the absorption, emission, or scattering of electromagnetic radiation by atoms or molecules to qualitatively or quantitatively study the atoms or molecules, or to study physical processes. The interaction of radiation with matter can cause redirection of the radiation and/or transitions between the energy levels of the atoms or molecules. A transition from a lower level to a higher level with transfer of energy from the radiation field to the atom or molecule is called absorption. Many compounds absorb ultraviolet or visible light, and thus appear colored to the eye; the degree of color being proportional to the concentration of the compound. Measuring the concentration of an absorbing species in a sample is accomplished by applying the Beer-Lambert Law.
The Beer-Lambert law is the linear relationship between absorbance and concentration of an absorber of electromagnetic radiation. Consider a beam of monochromatic radiation of intensity I0 going through a slab of sample solution of thickness dx which contains an absorber of electromagnetic radiation at a concentration C. Absorption takes place and the intensity of the beam of radiation leaving the sample has changed by some amount proportional to the thickness of the slab and concentration of the absorbing species.
where the coefficient α is a constant of the compound at a particular wavelenght of light. The wavelength at which given amount of a material absorbs light is the absorbance maximum, or λmax. This is the wavelenght at which the absorbance of a compund in solution is measured. We can rewrite the expression as a standard differential equation,
Integrating I over its range and dx over the thickness of the container,
In order to simplify things, we replace -α with [-α/2.303] and call it ε. As you already know, the 2.303 converts the natural log (ln) into log of base ten,
where b is the thickness of the solution and the log[If / Ii] term has been set equal to the quantity we call absorbance (A). Let's take a look at a beam of radiation passing through a substance or a solution, some of the light is absorbed and the remainder transmitted through the sample.
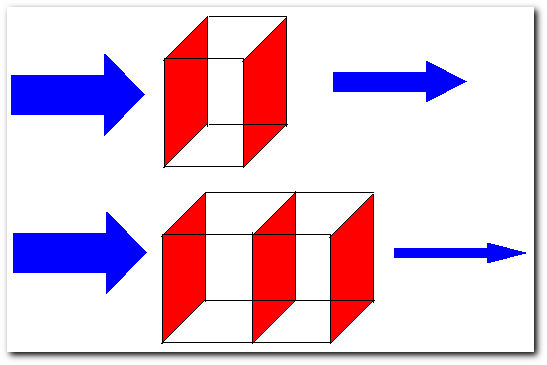
Light beams going through a solution. The thickness of the arrows are proportional the intensity of the beam.
Here, light beam number 1 (top) of intensity Ii goes through through a solution of concentration C and thickness b, the beam has an intensity smaller than Ii at the point of exit. Light beam number 2 (bottom) of the intensity Ii goes through the same solution, but this time there are two cells in the beam's path, meaning the thickness of the solution is ~2b, light beam number 2 comes out with an intensity even smaller than light beam number 1. The ratio of the intensity of the light entering the sample Ii to that exiting the sample If at a particular wavelength is defined as the transmittance (T). This is often expressed as the percent transmittance (%T), which is simply the transmittance multiplied by 100, for example: 3/4 = 75%, 1/2 = 50%, 1/4 = 25%, and so on. Thus the absorbance (A) of a sample is the negative logarithm of the transmittance.
The absorbance of a sample at a given wavelength is proportional to the absorptivity of the substance (a constant at each wavelength), the path length (the distance the light travels through the sample) and, in many instances, the concentration of the absorbing substance. In these cases the Beer-Lambert Law holds:
Commonly, ε and b are constant for a given set of experiments so that a plot of the sample absorbance as a function of concentration of the absorbing substance is a straight line. In practice, a calibration curve is prepared by plotting the absorbance of a series of standard samples as a function of their concentration. If the absorbance of an unknown sample is then measured, the concentration of the absorbing component can be determined from this graph.
Example of percent by mass using spectrometry
Ammonia can be determined spectrophotometrically by reaction with phenol in the presence of hypochlorite (OCl-) to yield a blue compound
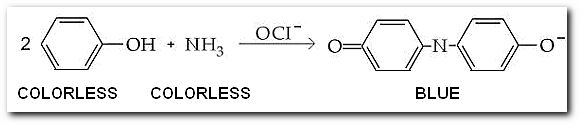
A series of standard solutions containing the blue compound were made by diluting a stock solution of NH4Cl, then reacting with phenol in the presence of hypochlorite to make a set of 100 mL solutions. The absorbance of each solution was measured at at 505 nm in a 1.00 cm cell.
A 0.048 g sample of certain nitrogen-containing compound was chemically digested to convert all of its nitrogen to ammonia, then treated with phenol and a sodium hypochlorite solution. The resulting blue solution was diluted to the mark in a 100 mL flask.
| Solution | Concentration of NH4Cl [g/L] |
Absorbance |
| Blank | 0.000 | 0.000 |
| 1 | 0.055 | 0.305 |
| 2 | 0.075 | 0.416 |
| 3 | 0.095 | 0.527 |
| 4 | 0.115 | 0.638 |
| unknown | ? | 0.584 |
Using this data, compute (a) the extinction coefficient ε of the blue compound including units and (b) the percent nitrogen by mass in the unknown compound.
The units of concentration are arbitrary, but it is very important that the units be included throughout the entire process. The extinction coefficient ε has units of [cm X concentration]-1. The actual number is meaningless without units.
The first step is to obtain the extinction coefficient, this is done by drawing the standard graph, the slope of the graph is ε.
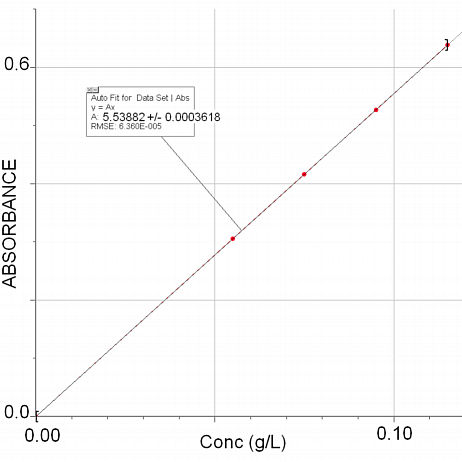
According to the graph output, f(X) = 5.53882X, this number is displayed in the top left corner of the graph and means that ε = 5.53882 [g/L]-1cm-1. If a compound is going to be converted into another, it is best to use mol/L as the concentration unit. Here, you are being asked to compute the percent nitrogen by mass, so it is best to use nitrogen as the reference frame. The solutions were prepared with NH4Cl, molar mass = 53.45 g/mol. To convert g/L to mol/L,
so the extinction coefficient in terms of mol/L of NH4Cl is
We multiply by the molar mass because ε has reciprocal units of concentration. Since there is one nitrogen atom in NH4Cl, this number is the extinction coefficient in terms of mol of nitrogen. The same is true for the blue compound because it has only one nitrogen.
Now we use the Beer-Lambert law to compute the molar concentration of the blue compound,
A = ε C b
0.584 = 296.0 [mol/L]-1cm-1 X C X 1.00 cm
0.584 / {296.0 [mol/L]-1cm-1 X 1.00 cm} = C = 1.97 X 10-3 mol/L
and since mol of N = mol of blue compound
mol of nitrogen = 1.97 X 10-3 mol X [100 X 10-3 L] = 1.97 X 10-4 mol
mass of Nitrogen = 1.97 X 10-4 mol X 14 g/mol = 2.76 X 10-3 grams
% N by mass = [2.76 X 10-3 grams / 0.048 grams] X 100 = 5.75%
EXPERIMENTAL PROCEDURE
Calibration Graph
Prepare five standard solutions. The concentration of Fe stock solution is 0.040 mg/mL. First, the following has to be added to all five solutions.
Then, each solution must be made different in iron content, these are the amounts of iron to be added and the concentrations you should use for your standard graph.
| Solution | mL of stock solution | mg of Fe | Fe concentration [mg/mL X 10-4] |
| Blank | 0.00 | 0.000 | 0.00 |
| 1 | 1.00 | 0.040 | 4.00 |
| 2 | 2.00 | 0.080 | 8.00 |
| 3 | 5.00 | 0.200 | 20.0 |
| 4 | 10.0 | 0.400 | 40.0 |
After adding all reagents, fill the flasks up to the 100.0 mL mark and let them stand for ~10 min. The blank solution will be used to calibrate the spectrophotometer. To do that:
Since the spectrophotometer is being calibrated in Transmittance mode, you should record the Transmittance of each solution and then convert to Absorbance using -log[T] = A. After you have your data, draw the calibration graph and determine ε from the slope. Remember to include units.
Determination of Iron in Scooby Vitamin Pill
The Scooby Vitamin Pill will be already dissolved in a beaker containing 40.0 mL of 6.0 M HCl. This volume is not important, all others from now on are. Now the pill must be diluted. Dilutions of solutions A and B refer to water only, solution C must include
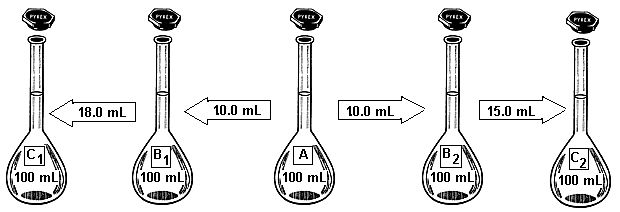
Dilution scheme for the Scooby Vitamin Pill
Dilute as indicated in the diagram, at the end we need to know the concentration of tablet per mL.
This is so because the entire tablet goes into flask A. Now take 10.0 mL of solution A and you get: [0.01 tablet/mL] X [10.0 mL] = 0.1 tablet
Take 18.0 mL of solution B1 and you get: [0.001 tablet/mL] X [18.0 mL] = 0.018 tablet
Take 15.0 mL of solution B2 and you get: [0.001 tablet/mL] X [15.0 mL] = 0.015 tablet
These are the recommended amounts, you can use different amounts as long as the difference is accounted for in the calculations.
Sample calculation
You must report [mg of Fe/tablet], lets assume that you got ε = 200 mg/mL-1cm-1.
Then you take solution C2 and find that the absorbance is 0.5923 in a 1.5 cm cell. First use Beer-Lamber law to get the concentration:
A = ε C b
0.5923 = 200 mg/mL-1cm-1 X [1.5 cm] X C
0.5923 / {200 mg/mL-1cm-1 X [1.5 cm]} = C
0.001974 (mg/mL) = C
and since the solution contains:
[0.015 tablet/100] = 0.00015 tablet/mL
The iron content per tablet is:
mg of Fe/tablet = [0.001974 (mg/mL)] / [0.00015 tablet/mL]
mg of FE/tablet = 13.16 mg Fe/tablet
But the cells we will be using have a 1.00 cm path length. So you would get for the above example that the Absorbance is 0.3923 and you will get the same answer at the end.