THE SI UNITS AND SIGNIFICANT DIGITS

The experimental protocol in chemical laboratories includes measurements of mass, volume, temperature, and other physical properties. These measurements are reported in either Base or Derived SI units.

Length and mass are base SI units; area, volume and density are derived SI units,

Volume = Length X Length X Length = Length3
density = Mass / Volume

In order for the SI units to follow a certain pattern, the kilogram and the cubic meter are the SI units of mass and volume respectively. However, these quantities are impractical for use in chemistry. Instead, the gram and the liter are most widely used. One gram is equal to 1 X 10-3 kg and one liter is equal to 1 X 10-3 cubic meters because 1 X 10-3 means 1/1000.

Example on density

A 180.0 kg sample of chemical Δ has a volume of 140.0 L. Compute the density of chemical Δ in g/cm3.

First let's get the number of grams:
180.0 kg X [103 g/kg] = 180.0 X 103 g of chemical Δ
Note that the units are treated as algebraic quantities and since [kg/kg] = 1, the kg units are said to cancel.

For the volume,
140.0 L X [ 103 cm3/L] = 140.0 X 103 cm3 of chemical Δ

And the density,
ρ(Δ) = [180.0 X 103 g] / [140.0 X 103 cm3] = 1.286 g/cm3

Depending on the task at hand, the values to be reported might be larger or smaller than the base SI units. Such quantities are written with prefixes that represent multiples of ten. Commonly used prefixes in the chemistry laboratory are:

PREFIX kilo centi mili micro nano
SYMBOL k c m μ n
POWER OF 10 103 10-2 10-3 10-6 10-9

Appropriate SI units (depending on their use) can be obtained by combining the base unit with a prefix. To change any of the resulting units of length into their equivalent values in meters use the appropriate operation and conversion factor.

Example using unit conversion

Due to the nature of the research and materials, small units are used in biotechnology. Some procedure indicates that you are to obtain 0.0500 mL of cultured cells suspended in buffer. Then add 75.0 μL of Lysozyme sulution (concentration 100 μg/mL) and 50.0 μL RNase A (concentration 500 μg/mL).
Compute (a) the total volume of the solution in liters, (b) the number of grams of Lysozyme and RNase A added (c) the mass of the entire solution in grams if its density is 1050 kg/m3. 

v(cells + buffer) = 0.0500 mL X [1 L/103 mL] 
v(cells + buffer) = 0.0500 X 10-3 L

v(Lysozyme solution) = 75.0 μL X [1 L/106 μL]

v(Lysozyme solution) = 75.0 X 10-6 L 

v(RNase A solution) = 50.0 μL X [1 L/106 μL] = 50.0 X 10-6 L

v(Total) = [0.0500 X 10-3 + 75.0 X 10 10-6 + 50.0 X 10-6] L 

v(Total) = 1.75 X 10-4 L

For the mass of Lysozyme, the units of density should match the units of volume. 
mL --> L = # of mL X 10-3

μg --> g = # of μg X 10-6

100 μg/mL --> 100 [g X 10-6]/[L X 10-3] = 0.100 g/L

m(Lysozyme) = 75.0 X 10-6 L X [.100 g/L] = 7.50 X 10-6 g

m(RNase A) = 50.0 X 10-6 L X [.500 g/L] = 25.0 X 10-6 g

For the mass of solution the units density should match the units of volume. Density is often reported in g/mL for liquids and g/cm3 for solids. The two expressions are equivalent,
1.0 mL = 1.0 cm3

Some conversion factors to use at the present time are:
m3 --> L = # of m3 X 103
L --> mL = # of L X 103
m3 --> mL or cm3 = # of m3 X 106
kg --> g = # of kg X 103
To convert 1050 kg/m3 to its g/cm3 equivalent, 

1050 kg = 1050 X 103 g

1.0 m3 = 1.0 X 106 cm3

1050 kg/m3 --> 1050 [g X 103]/[cm3 X 106] = 1.050 g/cm3

v(solution) = 1.75 X 10-4 L X [103mL/ L] = 0.175 mL or cm3

m(solution) = Volume X density = 0.175 cm3 X 1.050 g/cm3 

m(solution) = 0.18375 ~ 0.184 g

Note that the number has been rounded off to three significant digits. In order to understand significant digits, the measurements must be recorded properly. The typical biotechnology lab includes pipets that are accurate to the nearest μL and even smaller volumes. Some instruments are very easy to use because the measuring process is automated. A digital balance for example will make measurements at the actual uncertainty of the instrument and display the correct number of significant digits. Reading the volume on a graduated cylinder takes a lot more practice. For example, there are various types of graduated cylinder of 10 mL capacity. The volume readings to be reported depend on the number of graduations per unit volume. Some cylinders have graduations at 0.1 mL intervals so they have a 0.1 mL tolerance. Volumes should be reported to the nearest tenth of mL plus one more digit. This means that the number of mL is accurately known to the nearest tenth of mL because the liquid level is either above or below one of the graduations and the next digit is an estimate. If the graduations on the cylinder are more disperse, then the cylinder has a larger tolerance value and the readings will not be as accurate.

On the other hand, a high degree of certainty required to make an object that is to be used as a standard. Such an object would have to be ground down and measured with high precision calipers to within a certain tolerance. As a rule, there is an uncertainty of one unit in the last significant digit unless otherwise specified. So the number 1.000000 m is automatically assumed to mean 0.999999 or 1.000000 or 1.000001 m.

Example on building a standard

Due to unsettled differences with France, the United States of America decides to make its own length/mass standard in the form of a Titanium-Nickel alloy bar. The longest edge of the bar will be the meter standard and has been measured to be 1.000000 m. The width and height of the bar are 0.015000 m and 0.010000 m respectively. The mass of the bar is 1.00000 kg and will be the kg standard. Calculate the percent Titanium by mass in the bar. The density of Titanium is 4.51 g/cm3 and the density of nickel is 8.90 g/cm3. Assume volume additivity.


v(alloy bar) = 100 cm X 1.50 cm X 1.00 cm = 150 cm3 = 150 mL

Note that 1 mL = 1 cm3 so we can use either unit of volume. 


ρ(alloy bar) = 1000 g / 150 mL = 6.67 g/mL

ρ = M / V  -->  V = M / ρ

Total M / Average ρ = [M1 / ρ1] + [M2 / ρ2]

This means that the mass of Titanium plus the mass of Nickel has to equal the mass of the alloy, here 1000 g. It is simpler to set this value equal to 1 g, we could use 1000 g and still get the same answer because we are working with relative values. 

1000 g --> 1 g

M = 1 g = Total mass

M1 = &Psi = mass of Titanium

M2 = (1–Ψ) g = mass of Nickel 



1 g / 6.67 g/mL = [Ψ g / ρ1] + [(1-Ψ) g / ρ2]

1 g / 6.67 g/mL = [Ψ g / 4.51 g/mL] + [(1-Ψ) g / 8.90 g/mL]

The grams cancel and the Lowest Common Denominator is (4.51 X 8.90) 

  
0.150 mL X (4.51 X 8.90) =
Ψ X (4.51 X 8.90)   (1-Ψ) X (4.51 X 8.90)
----------------- + ---------------------
   (4.51) mL-1           (8.90) mL-1

6.02 mL =  [(Ψ X 8.90) mL] + 4.51 mL – [(Ψ X 4.51) mL]

6.02 mL - 4.51 mL =  [(Ψ X 8.90) mL] – [(Ψ X 4.51) mL]

1.51 mL =  Ψ X 4.39 mL  -->  1.51 mL / 4.39 mL =  Ψ = 0.344

% Titanium by mass = 34.4 %

The rules of significant digits apply to measured quantities which are non-exact. If a number is exact then there is no uncertainty and the number of significant digits is infinite. For example people, with the exception of half-wits, come in INTEGER numbers so there can be either 10 or 11 people but not 10.5.

GRAPHICAL ANALYSIS

Suppose, we know the general shape of a mathematical function, which seeks to analyze some relationship between two quantities by performing a series of measurements. For each measurement, we set some quantity X to a chosen value and measure the corresponding value of the quantity Y and represent these two points by a coordinate pair (X, Y) on a two dimensional grid. But need to figure out where each data point is to be placed specifically, and how to divide the axes. The following are some standard steps of the graphing procedure,

  • Include a complete, descriptive title for your graphs.
  • Sort the data points (smallest to largest) in a table of the ordinate (Y) and abscissa (X).
  • Scaled the graph axes so that the coordinate points (X,Y) are well distributed across the graph, covering as much of the paper as possible. The graph axes do not have to start at zero. This is what happens when if you don't start the axes at the correct value,

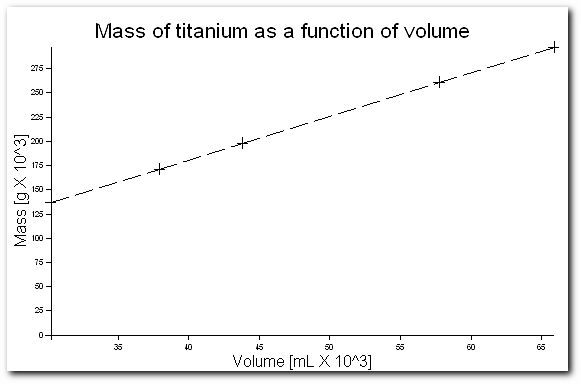
    Correcting this small problem we obtain,

    Note that if the axes of this graph had started at zero, only ~25% of the graph area would have been used.

  • Also note the error bars, here drawn as a '+'
  • Here, the axes have been labeled with the quantity plotted divided by the unit used: instead of writing 150000 grams, we write 150 and label the axis as [grams X 103].
  • Only a few labels need to be included: we label 150 then 175 instead of [150, 151, 152, 153, 154...], that would make the axes look messy. The few labels that you include should be equally spaced.
  • If drawing the graph by hand, make the smallest subdivision of the paper into whole numbers or simple fractional values of the unit being plotted. For example, if you make 20 subdivisions of the paper equal to 1 gram, then 5 subdivisions will be equal to 1/4 of a gram and one subdivision will be equal to 1/20 of a gram.
  • Error bars can also be drawn as circles around the data point. Remember when drawing graphs by hand that you are not connecting the dots, you are trying to draw the best straight line through the dots for linear functions and a smooth line for nonlinear functions...
  • When plotting two lines on the same graph, make one of them look different from the other. Here, one is solid and the other is a broken line. Note that a key has been included on one corner to help the reader distinguish between the two sets of data.
  • Some graphs span both, negative and positive ranges of a data set. That is why it is important to sort the data and decide as to the appropriate range that an axis is to span.
  • The slope of a straight-line graph is determined by choosing two points on the line of best fit, not just from any two points from the original data.