ENZYME KINETICS
Enzymes are macromolecules that, like all catalysts, speed up the rate of a chemical reaction without being used up in the process. The rate at which an enzyme works is influenced by several factors such as substrate concentration, temperature, pH and the presence of inhibitors. The substrate concentration factor can be explained in terms of collision theory: the more substrate molecules available, the quicker the enzyme molecules collide and bind with them. The temperature effect can be explained in terms of collision theory within a certain temperature range: molecular motion and hence collisions between enzyme and substrate speed up as the temperature rises but as enzymes are proteins, there is an upper limit beyond which the enzyme becomes denatured and ineffective. The pH of the medium affects protein conformation because certain amino acids become protonated/deprotonated at different pH, the effect is much more pronounced if the enzyme's active site contains these types of residues.
First proposed by Michaelis and Menten, the catalytic event that converts substrate to product involves the formation of a transition state. The complex that forms, when substrate and enzyme combine, is called the enzyme substrate (ES) complex.
k1
E + S <======> ES
k-1
k2 ES <======> EP k-2
Formation of the enzyme-substrate complex is fast and the decomposition of the complex to form products is relatively slow. In this experiment we will be concerned with the initial stages of product formation and the back reaction [E + P --> ES] can be ignored,
k1 k2 E + S <======> ES -------> E + P k-1 k-2=0
Given the conditions, the rate of product formation (R) is,
d[P] R = ------- = k2[ES] dt
In order to obtain an expression for [ES] we need to use the steady state approximation,
The instantaneous enzyme concentration [E] is not known as a function of time but an expression for it can be obtained as follows: because the enzyme is not being destroyed its total concentration [E]T is constant, the enzyme is either free [E] or bound [ES],d[ES]/dt = k1[E][S] - k-1[ES] - k2[ES] ≅ 0
[E]T[S] [ES] = ---------- [S] + Km
k2[E]T[S]
Rate = k2[ES] = ----------
[S] + Km
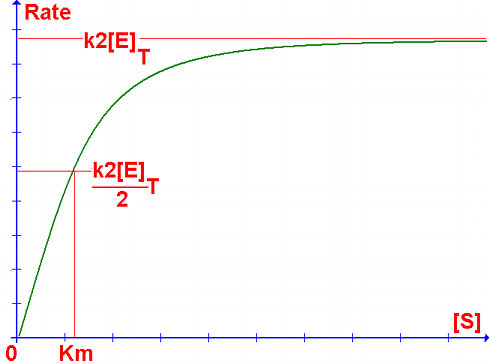
k2[E]T[S] R = ---------- Km
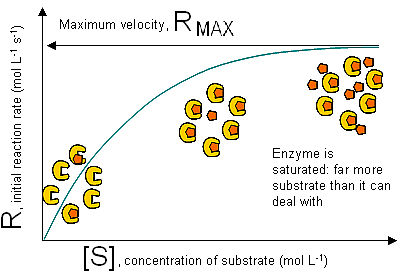
Very high substrate concentrations overwhelm the enzyme: all active sites are occupied, and the addition of further substrate does not increase the reaction rate.
The plot of Rate versus [S] above is not linear. Before the modern era of nonlinear curve-fitting on computers, this nonlinearity could make it difficult to estimate Km and Rmax accurately. Therefore, several researchers developed linearizations of the Michaelis-Menten equation, such as the Lineweaver–Burk plot and the Eadie-Hofstee diagram.
The Lineweaver–Burk plot or double reciprocal plot is a common way of illustrating kinetic data. This is produced by taking the reciprocal of both sides of the Michaelis–Menten equation,
1 Km 1
--- = -------- - ----
R Rmax[S] Rmax
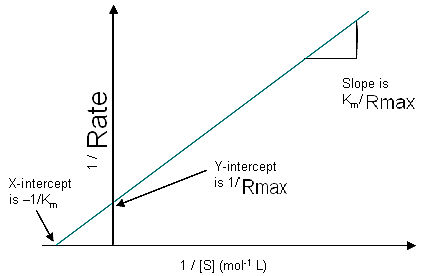
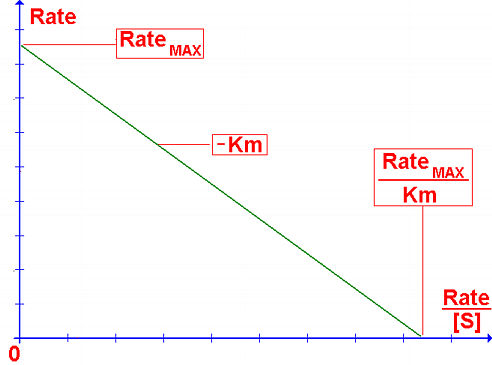
The Lineweaver–Burk plot skews the importance of measurements taken at low substrate concentrations and, thus, can yield inaccurate estimates of Rmax and Km. A more accurate linear plotting method is the Eadie-Hofstee plot. In this case, Rate is plotted against Rate/[S].
R k2[E]T R
--- = ----- - ----
[S] Km Km
Inhibitors affect the catalitic power of enzymes by binding to the same site as the substrate (competitive inhibition) or binding to some other site on the enzyme (noncompetitive inhibition). Irreversible inhibitors bind to the enzyme and destroy the active site, or otherwise screw the protein. Suicide inhibitors, a special class of such inhibitors, are activated by the normal catalytic activity of the enzyme, but form an intermediate that binds to and destroys the active site. Irreversible inhibitors bind tightly (often covalently) to the enzyme and cannot be removed by dialysis. They include such things as nerve gases (Sarin, DIPF, Tabun) and insecticides (Malathion).
KINETIC ANALYSIS OF TYROSINASE
Tyrosinase (EC 1.14.18.1) is a copper-containing enzyme present in plant and animal tissues that catalyzes the production of melanin and other pigments from tyrosine by oxidation. The three-dimensional structure of Tyrosinase from Streptomyces castaneoglobisporus exhibits a hydrophobic pocket adjoining a binuclear copper active site. One of the Copper atoms binds to the ε-nitrogen atoms of His38, His54, and His63. The other copper atom binds to the ε-nitrogen atoms of His190, His194, and His216. One probable catalytic mechanism has O2 getting trapped between the two copper atoms as one of the first steps in the reduction of molecular oxygen to water.
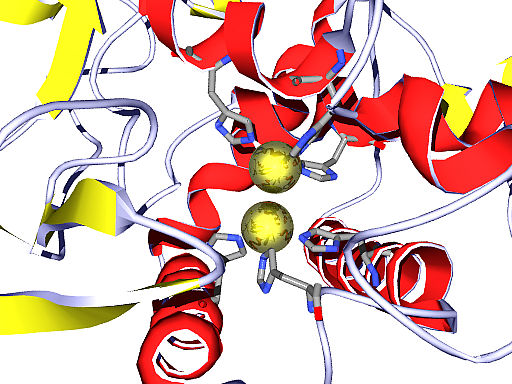
The active site of Tyrosinase. Each copper atom (gold sphere) is coordinated by three nitrogen donor atoms from histidine residues (shown in stick mode)
In this experiment, tyrosinase will be used to catalyze the conversion of DL-DOPA to hallachrome, a red compound which absorbs visible radiation at 475 nm,
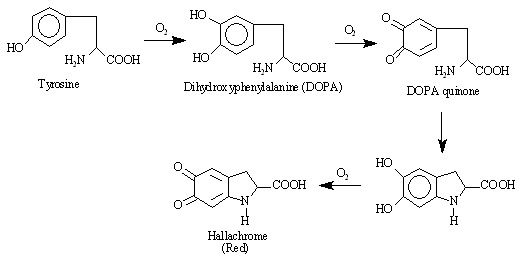
The reaction rate will be monitored by measuring the increase in absorbance at this wavelength that occurs as the reaction proceeds. The rate of the reaction will be determined for several different concentrations of substrate (DL-DOPA) with the concentration of enzyme (tyrosinase), pH, and temperature held constant for all runs.
Hallachrome is not the initial product of the oxidation of DOPA. However, the oxidation of DOPA to DOPA quinone is the rate determining step in the reaction sequence, and subsequent reactions occur very rapidly. Thus, the rate of formation of hallachrome is almost the same as the rate of formation of DOPA quinone.
REQUIRED MATERIALS AND APPARATUS
-spectrophotometer with computer interface or spectrophotometer + timer
-1.00 cm path lenght cells
-0.25 cm or small capacity quartz cells
-1000 μL pipets able to deliver at 100 μL increments
-Sodium Phosphate Buffer Materials
-Tyrosinase 100 units/mL
-L-DOPA 2mg/mL in Phosphate Buffer
-Thiourea 10-3 M in Phosphate Buffer
-Sodium Benzoate in Phosphate 3 X 10-3 M Buffer
EXPERIMENTAL PROCEDURE
Enzyme assays will be carried out on solution mixtures of 3.0 mL total volume. To prepare these solution mixtures, you will mix a precise volume of a stock solution of Tyrosinase with a precise volume of other solutions. For better results, solutions should be used the same day. If storage is required, store at 4 0 for no longer than three days and allow to warm to room temperature prior to use.
Compute the total enzyme concentration for the stock solution. An accurate measurement can be obtained from the extinction coefficient of tyrosinase at 280 nm. The Absorbance of a 1% (w/v) solution of pure tyrosinase 24.9 in a 1 cm cell. Using Beer-Lambert's law, the enzyme concentration is computed from a simple ratio,
C1% C
---------- = ---------
24.9(l cm) A(l)
Where C1% is the concentration of 1% (w/v) solution of pure tyrosinase, C is the concentration of unknown solution and l is the path lenght of the cell being used.
In order to collect data for one data set, the required quantity of DL-DOPA will be dissolved in a buffer solution in a cuvet and the reaction initiated by addition of the enzyme. The cuvet is then placed in a spectrometer, and the percent transmittance read every 15 seconds for 3 minutes. The reaction rate for the data set (Δhallachrome/second) can be determined by: [1] calculating the slope of the line which is nearly linear for the first part of the data set (Δabsorbance/second); [2] and dividing the slope by the molar absorptivity for hallachrome (5.00 X 103 M-1cm-1 at 475 nm) multiplied by the sample path length.
ΔA
ΔC = -------------------
5.00 X 103 M-1cm-1
Catalytic Activity Assay
Reagent 1 2 3 4 5 Buffer 1.45 1.40 1.30 1.10 0.70 L-DOPA 1.50 1.50 1.50 1.50 1.50 Tyrosinase 0.05 0.10 0.20 0.40 0.80
Michaelis-Menten Parameters
Reagent 1 2 3 4 5 Buffer 2.60 2.40 2.00 1.80 1.60 L-DOPA 0.20 0.40 0.80 1.00 1.20 Tyrosinase 0.20 0.20 0.20 0.20 0.20
Inhibition of Tyrosinase
Reagent 1 2 3 4 5 Buffer 2.50 2.30 1.90 1.70 1.50 L-DOPA 0.20 0.40 0.80 1.00 1.20 Inhibitor 0.10 0.10 0.10 0.10 0.10 Tyrosinase 0.20 0.20 0.20 0.20 0.20
DATA PROCESSING
-Plot absorbance as a function of time, draw the best straight line and determine the slope for all assays.
-Convert from Absorbance units to molar concentrations using the Beer-Lambert law and the extinction coefficient of Hallachrome.
-For the assay set where [E] is changing, plot the reaction rate as a function of enzyme concentration. Report the specific activity of the enzyme (μmol of product/min/mg of enzyme). Estimate enzyme's turnover number using your data and the molar mass of Tyrosinase (approx. 47 kDa).
-For the assay set where [S] is changing, make an Eadie-Hofstee plot of the data,
-Alternatively, you can do a double reciprocal plot of the data.
-Report Km, RateMAX, and the enzyme's turnover number. Compare the enzyme's turnover number with the estimate obtained using the specific activity. -Based on the Michaelis-Menten parameters obtained from the Tyrosinase inhibition assays, explain what kind of inhibitor compound X is.
-Download the structure of Tyrosinase [PDB code 1WX2], identify the residues in the active site. Based on your knowledge of ligand binding and protein structure, explain how the substrate binds the active site and propose a catalytic mechanism.
-Submit all graphs with your report.
THE GLUCOSE OXIDASE/HORSERADISH PEROXIDASE SYSTEM
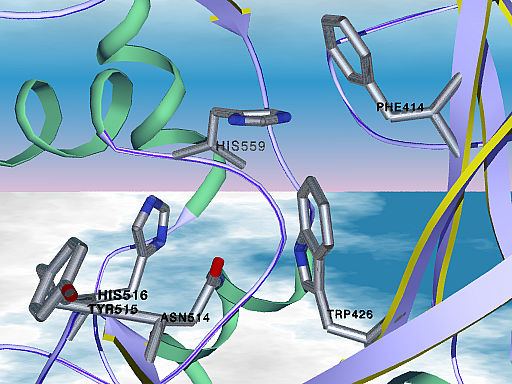
Glucose oxidase is a dimeric protein with a molecular weight of 160 kDa, containing one tightly bound flavin adenine dinucleotide (FAD) per monomer as cofactor. The apo-enzyme missing the FAD cofactor is not biocatalytically active, but it can be reconstituted with native or artificially modified FAD cofactor. The catalytic cavity includes Asp 584, Tyr 515, His 559 and His 516 which might be involved in the catalytic reaction or substrate binding. Additional contacts to the substrate might be formed by Phe 414, Trp 426 and Asn 514. Like other carbohydrate binding modules, aromatic residues are essential components of the catalytic cavity.
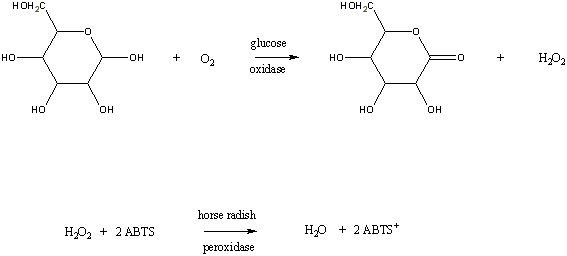
Glucose oxidase catalyzes the oxidation of β-D-Glucose by molecular oxygen to δ-Gluconolactone,
REQUIRED MATERIALS AND APPARATUS
-spectrophotometer with computer interface or spectrophotometer + timer
-2-2'-azino-bis(3-ethylbenzthiazoline-6-sulfonic acid)(Sigma catalog #A-1888)A
-Analytical grade β-D-glucose and D-mannose
-0.25 cm path lenght or small capacity cells [<2 mL]
-1000 μL pipets able to deliver at 100 μL increments
-Sodium Phosphate Buffer Materials
-Glucose oxidase (Sigma catalog #G-6125)B
-Horseradish peroxidase (Sigma catalog #P-6140)B
ACan be replaced with o-Dianisidine Reagent (Sigma catalog #D-2679)
BCan be replaced with lyophilizate Enzyme Reagent (Sigma catalog #G-3660)
EXPERIMENTAL PROCEDURE
Enzyme assays will be carried out on solution mixtures of 1.0 mL total volume. To prepare these solution mixtures, you will mix a precise volume of a stock solution of glucose oxidase with a precise volume of other solutions. For better results, solutions should be used the same day. If storage is required, store at 4 0 for no longer than three days and allow to warm to room temperature prior to use.
-Prepare a 0.1 M sodium phosphate buffer and adjust to pH 7.0
-Prepare an ABTS solution with a concentration of approximately 35 mM. As a rule of thumb, 20 mg (0.02 g) of ABTS reagent dissolved in 1.0 mL of deionized water will make a 35 mM ABTS solution.
-Prepare a HRP solution with a concentration of 25 Sigma units of HRP per mL.
-The Glucose oxidase stock solution should be about 5 Sigma units per mL. But this does not mean you should use this concentration. You should do a test run to see if this concentration gives an absorbance rate of change you can measure, if the solution changes color too fast or too slow you will not be able to get any meaningful data.
-The sugar (glucose and mannose) stock solutions should be 1.0 M.
Lets define assay α1/β1 as consisting of the following amounts of stock solutions: 600 μ of buffer, 100 μ of glucose oxidase, 100 μ of ABTS, 100 μ of HRP, and 100 μ of glucose. This gives final concentrations for glucose oxidase, ABTS, HRP, and glucose which are 10 times lower than the initial stock concentrations. Now you have to prepare assays where the enzyme concentration is varied, define assay α1/β1 as having enzyme concentration [E] and substrate (glucose) concentration [S], then you could prepare solutions that vary by some factor which is accessible with the Micropipets provided.
| α1 | α2 | α3 | α4 |
| [E] | [3E/4] | [E/4] | [E/8] |
| β1 | β2 | β3 | β4 |
| [S] | [3S/4] | [S/4] | [S/8] |
Similarly, the substitution to go from α1 to α3 is,
You get the idea, there are many possible variations for this experiment. The limiting factor is the volume increments that the Micropipets can deliver accurately.
The second week of the experiment, replace glucose with mannose. You will need about 2 mL of this solution and it has to be prepared on week one to allow for isomer equilibration. The concentration of glucose oxidase should be about 50-fold higher. Recall that glucose oxidase is specific for glucose and will exhibit slow oxidation rates for other sugars.
For each assay, monitor the absorbance for the first six minutes of the reaction. For spectrophtometers with a computer interface, set the machine to time monitoring mode and stop after 6 min. If the spectrophometer does not have a computer interface, record the absorbance at 20 sec intervals for 6 min. This is equivalent to monitoring the initial stages of product formation and the Michaelis-Menten plot will be linear during that time interval,
THE G3660 REAGENT CAPSULE & THE SIGMA UNITS
The Glucose Oxidase [a number of Sigma Units] and the Horseradish Peroxidase are contained in a capsule along with buffer salts [lyophilizate]. The Sigma Units are also a measure of activity per mg of enzyme:
The reagents in the capsule are medium grade. Just to give you an idea of what this means, the high grade enzyme has an activity of more than 200 Units/mg. A reasonable estimate of the enzyme in the capsule is about 20 Units/mg of Glucose Oxidase. Since the capsule contains 500 Units, we get
Then you can convert Units to mg using,
The instructor will place one capsule of Glucose Oxidase/Horseradish Peroxidase reagent [Sigma #G-3660] in a 25 mL volumetric flask to make a Master Solution for the whole class. The capsule contains 500 Units of catalytic strength which gives,
For each week of the experiment, you will need about 20 Units. The enzyme seems to have moderate speed with a stock solution of 5 Units/mL. Thus you can take 1 mL of the Master Solution in a mini beaker or vial and add 3 mL of deionized water to make your 5 Unit/mL stock solution. If you use 100 μL of your stock solution for a 1 mL assay, the working concentration of enzyme would be 1 Unit/mL. Then you can use 200 μL to make trial 2 equal to 2 Units/mL, and so on.
For the substrate [Glucose] variation, recall that you are using 100 or 200 μL of 1.0 M Glucose. That makes your working concentration 0.1 or 0.2 M, which is high enough NOT to affect the reaction rate. Thus you should dilute the 1.0 M solution. You can take 1 mL of the 1.0 M solution and add 4 mL of deionized water to make a 0.2 M Glucose.
2,2'-azino-bis(3-ethylbenzthiazoline-6-sulphonic acid) ABTS (green dye)
The dye works fine if the stock solution is about 30-40 mM. We want to use an amount we can measure accurately in the analytical balance. We can take 0.5 g of ABTS and dissolve in 25 mL of deionized water. Each assay will use 100 μL of dye, so this will be enough for the whole class. ABTS [diammonium salt] weights 548.68 g/mol which gives,
EXTINCTION COEFFICIENT OF O-DIANISIDINE
Hydrogen peroxide reacts with o-dianisidine in the presence of peroxidase to form a colored product. Oxidized o-dianisidine reacts with sulfuric acid to form a more stable colored product.
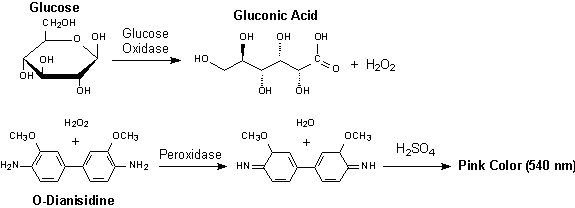
The modifications to the experimental procedure are if using o-dianisidine as the dye are:
For our enzyme kinetics experiment we do not need to use sulfuric acid. Instead, we can measure the absorbance of the brown colored oxidized o-dianisidine as it is generated. An absorbance wavelenght scan indicated that the oxidized o-dianisidine absorbs strongly at 440 nm. You could use a Beer-Lambert standard curve to figure out the extinction coefficient of o-dianisidine at this wavelenght. One way is to prepare standard glucose solutions, let the reaction go to completion and measure the absorbance. A group of students tried something different:
Four assays were done with high enzyme and substrate concentration. The concentration of the o-dianisidine dye was kept low. It is assumed that the dye will be used up completely. This means that the dye is the limiting reagent and the absorbance at 440 nm will be directly related to its concentration. We used the molar mass of o-dianisidine (244.29 g/mol) and the dilution factor to compute concentration C = 5.125 X 10-7.
CONC ABSORBANCE
C X 0 0
C X 0.25 0.27
C X 0.50 1.05
C X 0.75 1.77
C X 1.00 2.15
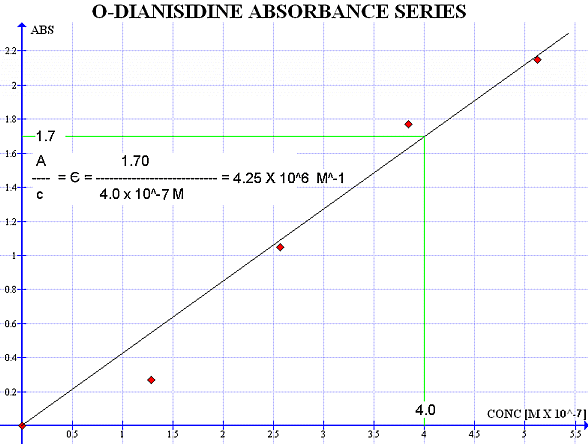
From the slope, the extinction coefficient is 4.25 X 106 M-1.
Thus to go from Absorbance to molar concentration you use:
Absorbance
Molar Concentration = ---------------
4.25 X 106 M-1
Thus the Absorbance units per second that you got from the spectrophotometer output become molar concentration per unit time (seconds). To convert the molar concentrations (mol/L) to moles (n) just multiply by the assay volume,
n = [mol/L] X 1 X 10-3 L
Because the assay volume is 1 mL.
DATA PROCESSING
-Compute the total enzyme concentration for the stock solution. An accurate measurement can be obtained from the flavin extinction coefficient (1.4 X 104 M-1cm-1) at 450 nm. Alternatively, you can use the definition of one Sigma unit: one unit will oxidize 1.0 μmole of β-D-Glucose per min at pH 5.1 and 35 0.
-Plot absorbance as a function of time, draw the best straight line and determine the slope for all assays.
-Convert from Absorbance units to molar concentrations using the Beer-Lambert law and the extinction coefficient of ABTS. The stoichiometry of the reaction is two molecules of ABTS oxidized for every molecule of glucose oxidized.
-For the assay set where [E] is changing, plot the reaction rate as a function of enzyme concentration. Report the specific activity of the enzyme (μmol of product/min/mg of enzyme). Estimate enzyme's turnover number using your data and the molar mass of Glucose Oxidase (160 kDa).
-For the assay set where [S] is changing, make an Eadie-Hofstee plot of the data. Alternatively, you can do a double reciprocal plot of the data.
-Report Km, RateMAX, and the enzyme's turnover number. Compare the enzyme's turnover number with the estimate obtained using the specific activity.
-The pH of the reaction mixture was 7.0 at all times. How would the oxidation rate change if the pH of the buffer was acidic? basic? Recall that (a) the initial product of glucose oxidation is D-glucono-1,5-lactone, a weak competitive inhibitor of Glucose Oxidase and (b) the native protein is acidic having an isoelectric point (pI) of 4.2.
-Download the structure of glucose oxidase [PDB code 1GAL], identify the residues in the active site. Based on your knowledge of ligand binding and protein structure, explain why the enzyme oxidized mannose is at a much slower rate than glucose.
-Submit all graphs with your report.


