|
|
The Chime image in the STRUCTURE section is actually one of a large collection of conformations with nearly equal stabilities.
 We are mostly interested in the chain of events from the time a photon is absorbed to the time its energy reaches the reaction center. The first of this chain of events is the absoption of a photon by a pigment molecule, and as a result one of its electrons gets promoted from its ground state molecular orbital to one of higher energy. In order for this process to occur the energy of the absorbed photon must exactly match the energy of the energy difference between two energy states of the pigment molecule. This constraint greatly limits the wavelenght range in which a molecule can absorb light. Light-harvesting complexes are constructed in a way as to solve this problem. The pigment molecules are embeded in the hydrophobic apoproteins, this changes the chemical properties of the pigment molecules so they can absorb light over a broader spectral range thus allowing more of the incident solar spectrum to be used productively[i5]. One way in which the apoproteins can do that is by changing the spectral range in which a pigment molecule absorbs light. As a result, the same pigment molecule can absorb at different wavelenghts depending on its interaction with the protein where it is embeded. Such is the situation for histidine-bacteriochlorophyll-carotenoid interactions. 
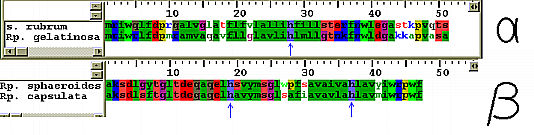 Location of the conserved histidine residues. The various avialable environments create differences in the absorbance bands of the pigment molecules. The resulting group of molecules not only absorb over a wider spectral range, the energy differences create some kind of funnel-like mechanism for energy transfer. Since energy travels towards areas of lower potential, the reaction center is sure to get all the energy it needs for photosynthesis. The figure below shows the relative energies of the different kinds of light-harvesting complexes. Put the cursor over the image to animate!  This animated gif illustrates the transfer of exitation energy towards the reaction center As it has already been pointed out; the absorption of a photon raises a pigment molecule to one of its higher excited states. 
The energy of a given excited state varies according to the environment where the pigment molecule is located. The relative energy and population of a given excited state may be further affected by the dialectric constant of the surrounding molecules, their abilility to form hydrogen bonds with the pigment molecules and the coordination sphere of the metallic center as in the magnesium core of a bacteriochlorophyll ring. What do all of the above factors have in common? It is clear that they tend to change the shape of molecules, this traslates into either creation or destruction of symmetry. Everyday experience tells us that when something goes up it has to come down unless energy is continuously supplied. There are many options avialable for the decay of an excited state. We are mostly interested with the two options that become avialable when several, slightly different species are present: transfer of energy to a molecule with an excited state of lower energy and transfer of an electron to or from the other molecule. The former may result in either sensitized fluorescence or another energy transfer, the latter is a transitory ion pair, which may under certain circumstances result in permanent chemical change[t11]. Energy transfer is, most of the time the first process that occurs after light absorption by pigment molecules. A simple model for energy transfer towards the reaction center was already illustrated in the previous sections. However, even if the energy reaches the reaction center, that does not guarantee an energy usage efficiency of nearly 100%. Sometimes the reaction center will be busy and the energy will not be absorbed. A model for transfer of exitation energy among more or less identical pigment molecules can be applied to explain how the photosynthetic unit deals with this kind of situation. An explanation can be generated with a computer simulated Random Walk. The master equations are listed at the bottom of this page. For this model it is assumed that a group of funnels are organized in domains of N funnels each. Energy can be tranfered among the lowest part of the funnels within a domain, but it is assumed that energy transfers between domains is absent. The first equation is the overall description of the process. There are two parameters upon which this process depends: The probabitity that the exitation is lost on a single transfer step and the probability that the exitation scapes after reaching a reaction center. These probabilities depend on a set of physical rate constants: kh, kl, and kt. Rate of transfer between reaction centers, rate of loss, and rate of exitation trapping respectively. In order to understand this kind of equation it is useful to to make one of the variables the defining parameter. The second equation shows the diffusion-limited case. Meaning that the exitation cannot escape from the reaction center. Notice that when that is the case, the probability of trapping (ft) and hence the the efficiency of energy usage is determined by the rate of exitation transfer and the rate of exitation loss. The third equation shows the trapping-limited case. The trapping probability is then controled by the rate of exitation loss and the rate of exitation trapping. Notice that a large rate of exitation loss will result in poor efficiency. The last equation summarizes the magnitude of energy loss. If the reaction centers were deactivated, then the quantity (ft) would be zero and all the energy would be lost. Computer simulations using the above described algorithms show that the quantum efficiency of photosynthetic units is nearly perfect.  |


